Himpunan biasanya dinotasikan dengan huruf besar A, B, C, X, A1, A2, dsb. Anggota suatu himpunan biasanya dinotasikan dengan huruf kecil a, b, c, x, x1, y, y1, dsb. Pernyataan a anggota A, dilambangkan dengan 
Himpunan dapat disajikan dengan cara:
1. Mendaftar anggota-anggotanya di dalam tanda kurung kurawal.
Contoh:
a. N adalah himpunan bilangan asli yang kurang dari lima disajikan dengan
N = {1, 2, 3, 4}.
b. P adalah himpunan konsonan yang membentuk kata “Jaringan” disajikan dengan
P = {j, r, g, n}.
c. H adalah himpunan pancaindra manusia disajikan dengan
H = {penciuman, perasa, pendengaran, penglihatan, peraba}
d. A adalah himpunan bilangan asli disajikan dengan
A = {1, 2, 3, 4, 5, ...}
e. B adalah himpunan bilangan bulat disajikan dengan
B = {..., -3, -2, -1, 0, 1, 2, 3, ...}
2. Menyajikan sifat-sifat anggotanya
Contoh:
a. A = {bilangan asli}
b. C = {bilangan cacah}
c. D = {bilangan bulat negatif}
d. E = {bilangan cacah yang kurang dari lima}
3. Menggunakan notasi pembentuk himpunan. Dengan cara ini himpunan disajikan dalam bentuk
{x | x bersifat R}, dibaca himpunan x di mana x bersifat R.
Contoh:
a. Himpunan A di atas disajikan dengan
A = {x | x adalah bilangan asli}.
b. Himpunan E di atas disajikan dengan
E = {x | x adalah bilangan cacah dan x < 5}.
Himpunan yang tidak mempunyai anggota dinamakan himpunan kosong dan dinotasikan dengan {}.
Contoh himpunan kosong:
1. Himpunan mahasiswa yang berat badannya lebih dari 1 ton.
2. Himpunan maling yang tak pernah mencuri.
3. Himpunan bilangan cacah negatif.
Banyak anggota dari himpunan A dinotasikan dengan n(A).
Contoh: n({1, 2, 3, 4}) = 4,
n{} = 0,
n({bilangan asli}) = tak terhingga
Himpunan yang banyak anggotanya berhingga (finit) disebut himpunan berhingga. Sebaliknya himpunan yang banyak anggotanya tak terhingga, misalnya {bilangan asli}. Disebut himpunan tak hingga (infinit).
Catatan:
Himpunan semua obyek yang sedang dibicarakan disebut himpunan semesta dan dinotasikan dengan S atau U. Himpunan semesta harus kita tentukan dahulu sebelum kita membicarakan himpunan objek dengan sifat-sifat yang lebih khusus.
Contoh:
S = {bilangan asli}
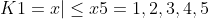
K2 = {x | x2 + x = 2} = {1}
K3 = {x | x < 1} = {}
Himpunan dapat disajikan dengan cara:
1. Mendaftar anggota-anggotanya di dalam tanda kurung kurawal.
Contoh:
a. N adalah himpunan bilangan asli yang kurang dari lima disajikan dengan
N = {1, 2, 3, 4}.
b. P adalah himpunan konsonan yang membentuk kata “Jaringan” disajikan dengan
P = {j, r, g, n}.
c. H adalah himpunan pancaindra manusia disajikan dengan
H = {penciuman, perasa, pendengaran, penglihatan, peraba}
d. A adalah himpunan bilangan asli disajikan dengan
A = {1, 2, 3, 4, 5, ...}
e. B adalah himpunan bilangan bulat disajikan dengan
B = {..., -3, -2, -1, 0, 1, 2, 3, ...}
2. Menyajikan sifat-sifat anggotanya
Contoh:
a. A = {bilangan asli}
b. C = {bilangan cacah}
c. D = {bilangan bulat negatif}
d. E = {bilangan cacah yang kurang dari lima}
3. Menggunakan notasi pembentuk himpunan. Dengan cara ini himpunan disajikan dalam bentuk
{x | x bersifat R}, dibaca himpunan x di mana x bersifat R.
Contoh:
a. Himpunan A di atas disajikan dengan
A = {x | x adalah bilangan asli}.
b. Himpunan E di atas disajikan dengan
E = {x | x adalah bilangan cacah dan x < 5}.
Himpunan yang tidak mempunyai anggota dinamakan himpunan kosong dan dinotasikan dengan {}.
Contoh himpunan kosong:
1. Himpunan mahasiswa yang berat badannya lebih dari 1 ton.
2. Himpunan maling yang tak pernah mencuri.
3. Himpunan bilangan cacah negatif.
Banyak anggota dari himpunan A dinotasikan dengan n(A).
Contoh: n({1, 2, 3, 4}) = 4,
n{} = 0,
n({bilangan asli}) = tak terhingga
Himpunan yang banyak anggotanya berhingga (finit) disebut himpunan berhingga. Sebaliknya himpunan yang banyak anggotanya tak terhingga, misalnya {bilangan asli}. Disebut himpunan tak hingga (infinit).
Catatan:
Himpunan semua obyek yang sedang dibicarakan disebut himpunan semesta dan dinotasikan dengan S atau U. Himpunan semesta harus kita tentukan dahulu sebelum kita membicarakan himpunan objek dengan sifat-sifat yang lebih khusus.
Contoh:
S = {bilangan asli}
K2 = {x | x2 + x = 2} = {1}
K3 = {x | x < 1} = {}

9 komentar:
K2 = {x | x2 + x = 2} = {1}
x2 + x = 2 <> 3x = 2 <> x = 2/3
seharusnya begini...
kita juga punya nih artikel mengenai 'Himpunan', silahkan dikunjungi dan dibaca , berikut linknya
http://repository.gunadarma.ac.id/bitstream/123456789/6515/1/Indikasi%20Bahwa%20Objek-Objek%20Matematika%20Dapat%20Dipandang%20Sebagai%20Barisan%20Struktur-struktur%20Hingga.pdf
trimakasih
semoga bermanfaat
makasih, saya sudah lumayan ngerti sekarang
terimakasih sudah dapat membantu, kalo bisa lbh dilengkapi lagi
terimakasih sudah dapat membantu, kalo bisa lbh dilengkapi lagi
Lolz
Lolz
Kurang jelas
hi, halo. p={1,4,9,16,36} notasinya gimana ya? gracias
Post a Comment