Elemen lingkaran
Elemen-elemen yang terdapat pada lingkaran, yaitu :
- Elemen lingkaran yang berupa titik, yaitu :
- Titik pusat (P)
merupakan titik tengah lingkaran, dimana jarak titik tersebut dengan titik manapun pada lingkaran selalu tetap - Elemen lingkaran yang berupa garisan, yaitu :
- Jari-jari (R)
merupakan garis lurus yang menghubungkan titik pusat dengan lingkaran. - Tali busur (TB)
merupakan garis lurus di dalam lingkaran yang memotong lingkaran pada dua titik yang berbeda. - Busur (B)
merupakan garis lengkung baik terbuka, maupun tertutup yang berimpit dengan lingkaran. - Keliling lingkaran (K)
merupakan busur terpanjang pada lingkaran. - Diameter (D)
merupakan tali busur terbesar yang panjangnya adalah dua kali dari jari-jarinya. Diameter ini membagi lingkaran sama luas. - Apotema
merupakan garis terpendek antara tali busur dan pusat lingkaran.
- Jari-jari (R)
- Titik pusat (P)
- Elemen lingkaran yang berupa luasan, yaitu :
- Juring (J)
merupakan daerah pada lingkaran yang dibatasi oleh busur dan dua buah jari-jari yang berada pada kedua ujungnya. - Tembereng (T)
merupakan daerah pada lingkaran yang dibatasi oleh sebuah busur dengan tali busurnya. - Cakram (C)
merupakan semua daerah yang berada di dalam lingkaran. Luasnya yaitu jari-jari kuadrat dikalikan dengan pi. Cakram merupakan juring terbesar.
- Juring (J)
[sunting]Persamaan
Suatu lingkaran memiliki persamaan
dengan  adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan  adalah koordinat pusat lingkaran.
adalah koordinat pusat lingkaran.
 adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan  adalah koordinat pusat lingkaran.
adalah koordinat pusat lingkaran.
Jika pusat lingkaran terdapat di 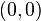 , maka persamaan di atas dapat dituliskan sebagai
, maka persamaan di atas dapat dituliskan sebagai
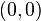 , maka persamaan di atas dapat dituliskan sebagai
, maka persamaan di atas dapat dituliskan sebagai
Bentuk persamaan lingkaran dapat dijabarkan juga menjadi bentuk
dengan  adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan  adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.
adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.
 adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan  adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.
adalah koordinat pusat lingkaran. Bentuk persamaan tersebut dikenal sebagai bentuk umum persamaan lingkaran.[sunting]Persamaan parametri
Lingkaran dapat pula dirumuskan dalam suatu persamaan parameterik, yaitu
yang apabila dibiarkan menjalani t akan dibuat suatu lintasan berbentuk lingkaran dalam ruang x-y.






0 komentar:
Post a Comment